MainPage:Nuclear:Summer2017:Blessed
Commissioning of a crystal drawing system
Abstract
Text.
Introduction
Lead Tungsten crystals have been found to be very effective in particle energy measurements and thus, the continuous developments in nuclear physics. This is because the crystals have have favorable properties such as:
1.Relatively high light yield:
2.Small Moliere radius:
This is a constant/property of a material which gives the scale of the transverse dimension of the fully contained electromagnetic showers(initiated when a high-energy electron, positron or photon enters a material resulting in either the photoelectric effect, Compton scattering or pair production. All this depends on the energy of the primary particle.) It can simply be defined as the radius of a cylinder containing an average of 90% of the shower's energy deposition.
3.Short radiation length:
This is the mean distance that a high-energy particle travels before losing 1/e of its energy by bremsstrahlung. One would expect that this distance be dependent on the energy of the particle but it only depends on the mass number and atomic number of the material.
However, manufacturing of Lead-Tungsten crystals has yet to be perfected and there has been considerate variation in the properties of the produced crystals. In this project, we aim to build a prototype for the manufacturing of these crystals locally by the Czochralski method. In building this prototype, the behaviour of the mechanical set-up is critical due to the sensitivity introduced by the above method. During the process of making the crystals, the rod needs to be rotated at 35rpm in order to maintain a sufficient mixture of the melt. So that it doesn't fall back into crucible? This rotation introduces some vibrations into the system, along the vibration of the surface the set-up is on or the building in general.
Description of the crystal drawing apparatus
Text.
Vibration Studies
As mentioned in the introduction, we need to damp the system so that the vibrations don't affect the highly sensitive temperature gradient of the mixture. Now, we will determine the amount of vibrations that are introduced to our set-up by the rotation using an Adruino board and an ADXL3xx accelerometer. Before this can be done, we need to calibrate this hardware.
Calibration of the accelerometer:
The accelerometer measures proper acceleration and can be calibrated using known values of the gravitational acceleration on the surface of the earth. We connect the Arduino board to the accelerometer as can be seen from the following figure and we allow the accelerometer to draw its input voltage from the output of the digital output pins cause it uses very little current.
Due to the high sensitivity of the accelerometer, we have to attach it to a heavy metal to ensure that it doesn't move. To do this, the accelerometer was placed inside a ............ then taped to an iron metal block as can be seen in the figure below. Now, the problem that arise here is that this block was uneven and this tilted the accelerometer by different angles for different orientations. A gravity linear....... was used to measure the length of the sides which were then used to calculate the angle of tilt.
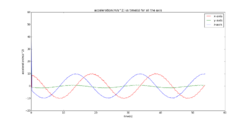
The next step is to collect results after attaching the set-up to a laptop. To do this, some software and programming is required. The code for the arduino board can be found here............ and it measures readings from all 3-axes of the accelerometer. Arduino prints out the output values from each axis to the screen and we need a software that will print these values to a file saved on a computer. For this reason, Gobetwino was installed. Gobetwino is ................. Data needs to be collected with all 3-axes aligned and anti-aligned with gravity with the equipment stationery. The plot below shows the values measured by the accelerometer vs time and we can see that they are constant which is parallel to the fact that gravitational acceleration is constant near the surface of the earth.
To analyse the data, VPython was used. We know that the measurement of the accelerometer is proportional to the acceleration signal and so, a linear model/relation would be appropriate here such that ACCELERATION = A*SIGNAL + B. Here A and B are constants which will be determined as follows: let SIGNAL be the average of the values measured by the accelerometer and let ACCELERATION be +9.8(gravity) when gravity is aligned with the +axis and -9.8 when gravity is anti-aligned with the -axes then solve the following equations.
+9.8 = A*+SIG + B
-9.8 = A*-SIG + B
Calibration needs to be done separately for different axis. The code that was used to obtain these constants can be found here...... for the x-axis and it's error, similarly, you can find A and B for the y and z axis with the errors. Uncertainties were obtained from using the angle of tilt that was mentioned earlier. The results of the calibration are tabulated below:
| X | Y | Z | |
|---|---|---|---|
| A | -0.14767501 | -0.14689038 | -0.14759584 |
| B | 49.83232499 | 49.28610738 | 51.09182802 |
| Deviation percentage | 0.0816326530612 % | 0.0714285714286 % | 0.0510204081633 % |
calibration of the accelerometer:
misalignment angle measured gravity deviation percentage
2.26245953203 degrees, 9.80764530293 m/s^2, 0.0816326530612 % for the x-axis
2.11138229046 degrees, 9.80665779414 m/s^2, 0.0714285714286 % for the y-axis
1.88511051001 degrees, 9.80530664911 m/s^2, 0.0510204081633 % for the z-axis
Rotation Studies
Text.
Calibration of the load cell
Text.