MainPage:Nuclear:Summer2016:12GeVExp

Elastic Analysis, at CUA

File:123.pdf

Abstract

Previously, scientists believed pions and kaons, particles that constitute matter, were points without structure. With new research that theory has been proven incorrect. Next year Catholic University of America at Jefferson Lab will conduct a kaon experiment. The goal being to detect kaons with the Gas Cherenkov Detector of the High Momentum Spectrometer (HMS). The HMS measures the particles scattered by the electron when it hits the target proton. With this particle detection they hope detect, predict, and study the kaon particle’s form factor. In Addition, the experiment can be set up to detect both kaons and pions. This preferred set up that detects both kaons and pions will allow the researchers to study the Pion’s form factor as well. In order for both particles to be studied, the experiment must be optimized and set up correctly. To optimize the experiment code was typed and data analysis was used to determine the proper set up. Once, a simulation was run using previous data collected from a similar experiment at the Jefferson Lab. Then the total number of events from the similar experiment and simulation were plotted onto a histogram. Code was written in root that normalized and cut both data sets allowing them to be compared. The normalized data confirmed that the number of events was equal to the number of electrons sent or the actual yield. By studying the graphs insight into which aspects of the experiment to be done next year were optimized could be instituted such as different materials, angels, or methods. By detecting both sub atomic particles the experiment had the best chance to discover each particles form factor.

Personal Contribution Statement

During my summer internship with CUA (Catholic University of America) I ran simulations from previous trials. I then graphed the simulations with the previous results on a histogram. I tested and created code through CERN’s root program that normalized and cut the histograms. This allowed for it to be compared. It also confirmed the actual yield where the input equals the output. The comparison also allowed me to suggest where improvements could have been made by looking at where certain data was different than predicted. I helped to optimize the set up to best detect both kaons and pions.

Validating the Simulation with Previous Elastic data from Hall C

A Monte Carlo simulation, which is used to predict the probability of certain outcomes of events, needed to be validated in order to be used for the Kaon experiment set to run next year. As the Kaon experiment is completely theoretical, the simulation needs to give an accurate number of kaons and pions. Without an accurate number we would not be able to predict whether or not we could have insights into the pion form factor.

First, four input forms were created to mimic previously done elastic scattering experiments at JLab. The simulation was set up to track the scattered electron in the HMS (High Momentum Spectrometer) similar to the experiment.

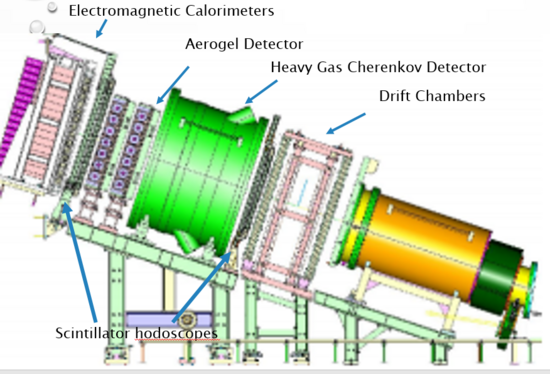
Particle detection

Various particles can be detected in the HMS and SHMS (Super High Momentum Spectrometer).

fig 1:

Shown above are the particle identification detectors within the spectrometers. To detect electrons use: gas Cherenkov detector and the electromagnetic calorimeter. For Kaon and Pion detection use: the Heavy Gas Cherenkov and the Aerogel Detector. The other detectors such as the Drift Chambers are used for particle trajectories, whereas the scintillator hodoscopes are used for for timing.

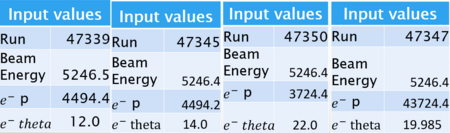
Table 1:

The various input values are shown above. By changing the election momentum and angle, we can better learn our spectrometer.

Preliminary Results: shown below is a graph containing the simulations result superposed with the experimental recorded data.

The Graph only contains weights, normfac, and the prescale. The normfac accounts for the proper cross section. The prescale is needed because the computers can only pick up so many particles at once. Instead, it will measure for example one particle for every eighty that pass through to avoid crashing. Therefore the experimental data must be multiplied by eighty in this case to get the actual amount of data points. No cuts have been applied to the simulation's data.

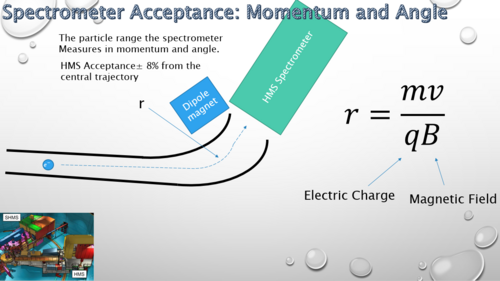
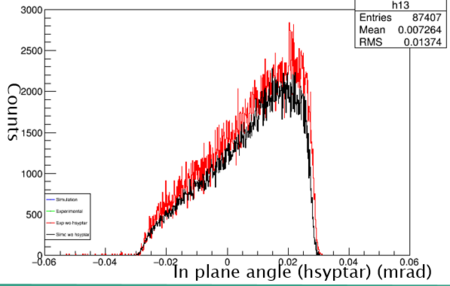
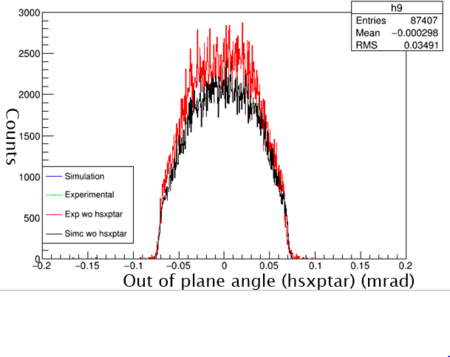
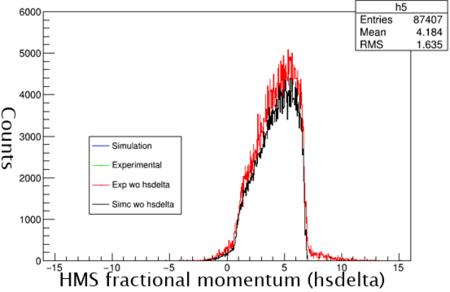
Next cuts needed to be applied to the simulation. The HMS can only accept a particle within certain ranges. The ranges are the hsxptar, hsyptar, and the hsdelta. The hsxptar (out of plane angle) contains the horizontal plane angle acceptance that the electron follows as it heads into the spectrometer. The cut for hsxptar is plus or minus .09 mrad from the center path(better phrase needed). The hsyptar (in plane angle) is the vertical planar acceptance into the spectrometer. The hsyptar acceptance is plus or minus 0.024 mrad from the center path(still better phrase). Finally, the electron must be bent into the the HMS. This is the hsdelta cut.

fig 1:

Shown below is the formula for the hsdelta cut. The particle acceptance depends on the particles momentum. r represents the radius of the curve that the electron is bent around into the spectrometer. The spectrometer acceptance is plus or minus 8% from the center curve.

Cuts are applied to the simulation data because without them every particle is accepted. The cuts must be applied to take into account what the spectrometers at JLab accept to get the most accurate simulation of what will actually happen. The process of cutting removes the data points which fall outside of the specified range.

Graph 2:

Shown above is the hsyptar data with cuts applied. The two data sets are very similar, in which with cuts applied both are accepting very similar amounts of particles.

Graph 3:

Shown above is the hsxptar data with cuts applied. The two data sets are very similar, in which with cuts applied both are accepting very similar amounts of particles.

Graph 4:

Shown above is the hsdelta with cuts applied. The two data sets are very similar, in which with cuts applied both are accepting very similar amounts of particles.

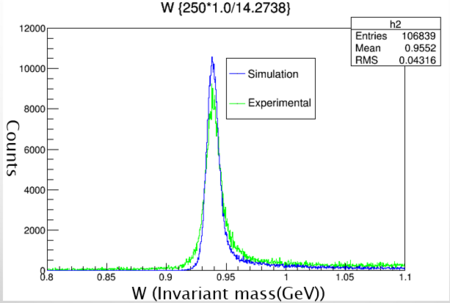
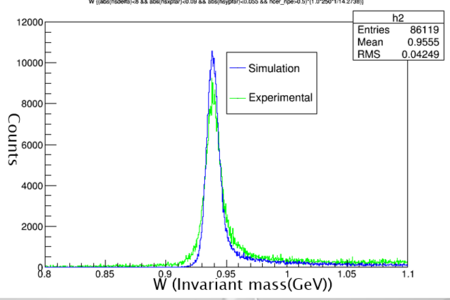
Graph 5:

Shown above is a histogram with W (invariant mass) plotted from the 47339 trial. The peak should be at the GeV of a proton 0.94 which it is. This means the simulation has gone correctly so far.

Particle Detection (Calorimeter and Gas Cherenkov Detector)

Both the detectors detect electrons. The Heavy Gas Cherenkov Detector contains a heavy gas on the inside. The electron passes through the gas faster than the speed light does. In turn, the particle gives off Cerenkov radiation (Blue light) which is picked up by the detector and measured in photo electrons. The Calorimeter works by measuring the particle's energy as it passes through the detector.

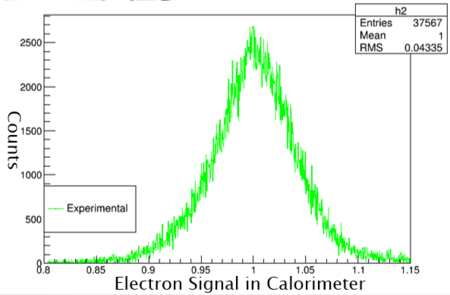
Graph 5:

Shown above are the readings from the Calorimeter. Since there is only a peak at one and no other peaks no other particles than the electron are being detected.

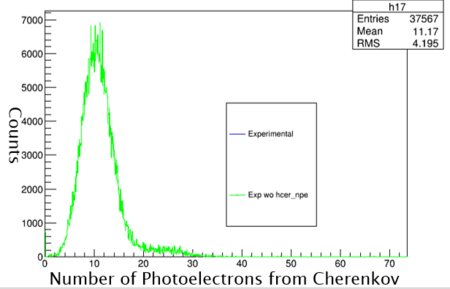
Graph 6:

Shown above is the number of counts for each number of photo electrons. One electron emits ten photo electrons in the Gas Cherenkov Detector. Since only electrons are being detected there is no cross contamination from pions or other sub-atomic particles.

Validation

After applying all of the cuts and determining there was no cross contamination we progressed onto validating the simulation. In order to do so we divided the experimental yield by the simc yield. Theoretically we would get one if the simulation was the same as the experiment. To determine the statistical uncertainty we used a poisson distribution.

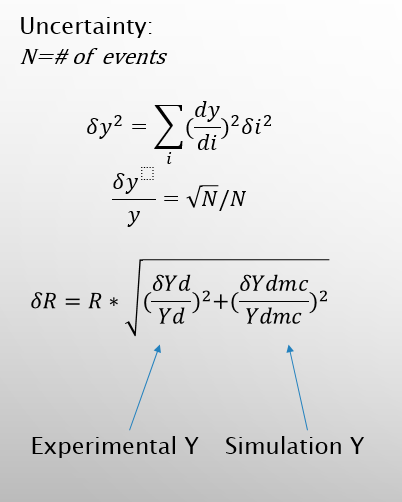
fig 2:

Shown above is the uncertainty formula used. The derivative for the simulation and experiment simplifies to the square root of the number of events divided by the number of events. Then those number are squared and then added together. Then the square root of the new new is taken and multiplied by its r value.

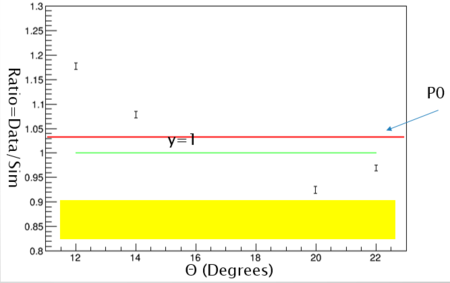
Shown above The r value is graphed with its respective theta (angle). The P0 line displays the line the points form. The line is very close to y=1 and within the error. The error bars represent the statistical error and error band the systematic. The r values are very close to one and the simulation is validated. It can now be used to make predictions for the kaon experiment.

Introduction

Since we validated the simulation we can now use it to predict the number of kaons we will detect from our kaon experiment. The experiment takes place next year. No experimental data has been collected yet. We hope to also determine the number of free pions (pions we are able to detect during the kaon experiment) we should detect and if there are enough pions created to study their form factor.

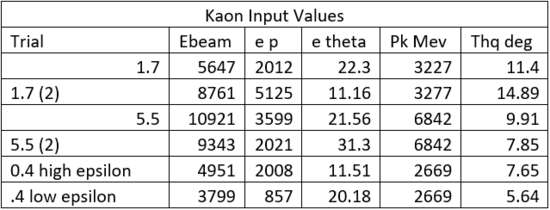
Input forms

Shown above are the values that will be used in the experiment at JLab next year. For this simulation we were detecting kaons.

SHMS

To detect Kaons we use the SHMS (Super High Momentum Spectrometer), which is new to JLab. The SHMS replaced the SOS spectrometer. The SHMS uses a similar PID set up to detect the particles that result from the reaction. Furthermore, we must apply cuts to out data to account for the SHMS acceptance.

SHMS Cuts

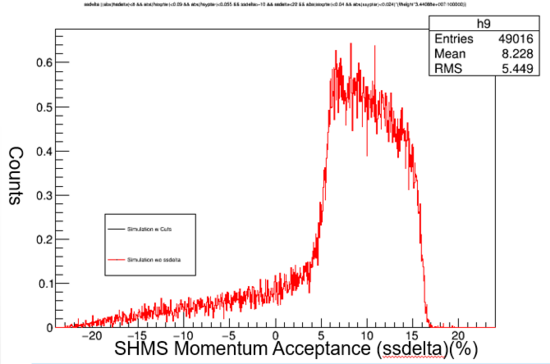
The cuts applied to the simulation's data most inlclude the HMS acceptance and the SHMS acceptance. Shown below are the cuts from the SHMS. The HMS cuts follow the same procedure as shown above while validating the simulation. The ssdelta, ssxptar, and ssyptar are located in the place as the HMS, but now apply to the SHMS. Shown below are the cuts applied to the 1.7 GeV run. The same cuts were applied to all of the other runs as well.

Graph 1:

Shown above is ssdelta data with and without the cut. The black line represents the data with the cuts applied -10% to 22%. The percentage is shown on the x axis. The data outside the cut would no be accepted by the spectrometer. The cuts allow for better prediction of what we expect to yield.

Graph 2:

Shown above is the ssyptar data with and without the cut. The acceptance is plus or minus 0.024 mrad and is graphed on the X-axis. Outside the acceptance would not be recorded by the spectrometer and with the cut it is not accepted by the simulation as well. The red line represents the data with cuts applied.

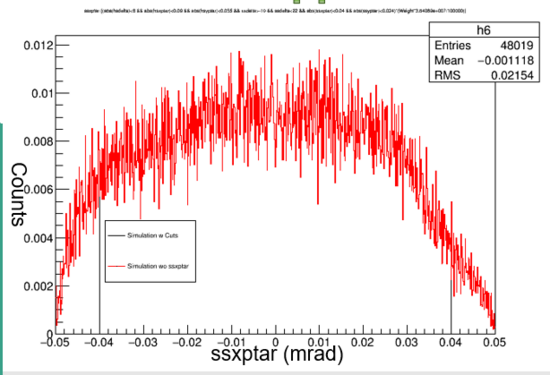
Graph 3:

Shown above is the ssxptar data with and without the cut. The acceptance is plus or minus 0.04 mrad and is graphed on the X-axis. Outside the acceptance would not be recorded by the spectrometer and with the cut it is not accepted by the simulation as well. The black line represents the data with cuts applied.

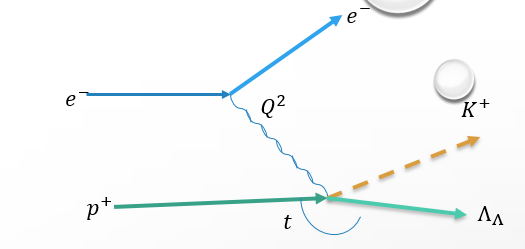
Fig 1:

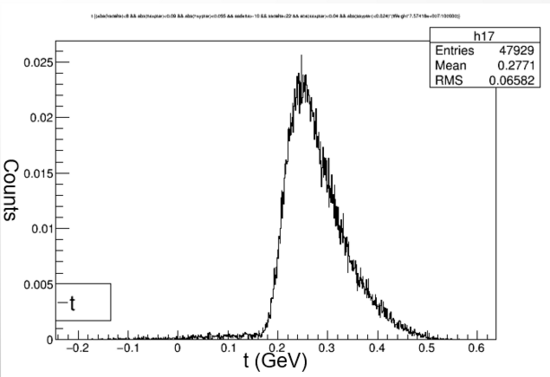
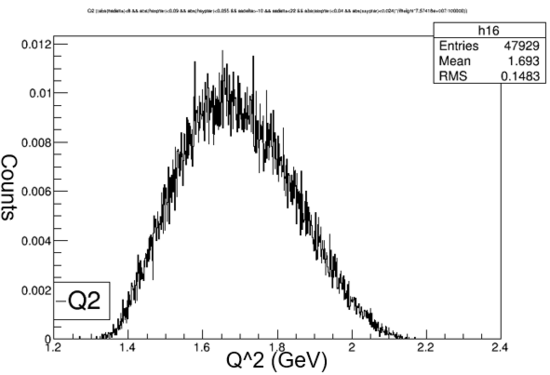
Shown above is a diagram showing the simplified Kaon reaction with the graphs of Q2 and t. Q2 represents the energy added by the electron to the reaction. t represents the energy added by the proton to the reaction. When the reaction occurs kaons are not the only particles created. Lambda represents the other particles that are needed in order to meet the conservation of momentum laws.

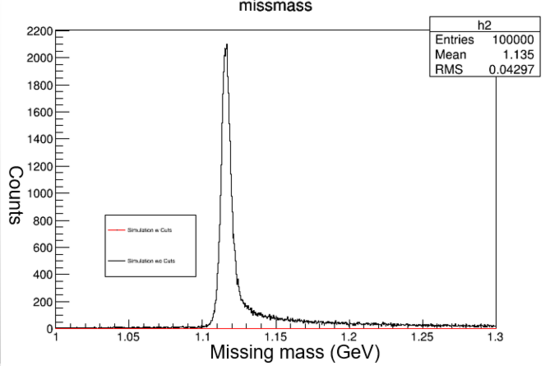
Graph 4:

Shown above is the missing mass with all of the cuts applied (red line). The missing mass is graphed on the X-axis and counts on the Y-axis. The missing mass represents the mass needed in order to satisfy the conservation of momentum laws. It is the mass not detected by the spectrometer. Both the HMS and SHMS cuts are applied. The yield is very small, but when zoomed in a visible peak appears at 1.115 or the mass of Lambda. The lambda mass verifys that the simulation correctly produced the kaon electro production reaction because distribution should be centered on the Lambda mass (~1.115 GeV).